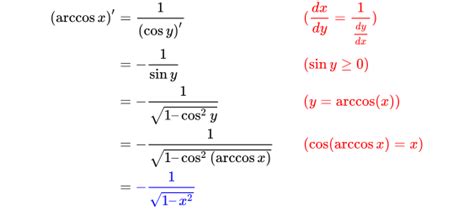直角三角形边长求三角度,轻松学会!
在几何学中,直角三角形是一种具有一个90度角(即直角)的三角形。这种三角形在许多实际应用中都非常重要,比如在建筑、工程以及天文学等领域。当我们知道直角三角形的三条边长度时,可以利用这些信息来计算三角形的三个角度。本文将详细介绍如何使用直角三角形的三条边来计算其三个角度。
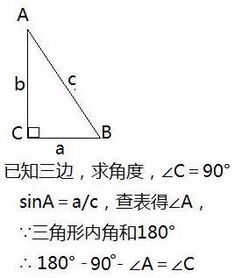
首先,我们需要明确直角三角形的三条边:直角边(两条与直角相邻的边)和斜边(最长的一条边,与直角相对)。在计算角度时,最常用的方法是利用三角比(trigonometric ratios)或者反三角函数(inverse trigonometric functions)。
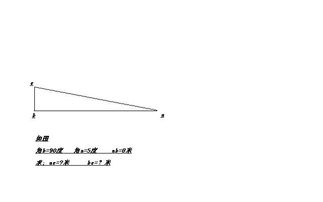
1. 使用三角比计算角度
三角比是直角三角形边长之间的比例关系,这些比例关系定义了正弦(sine)、余弦(cosine)和正切(tangent)三个基本三角函数。对于直角三角形,我们可以将这些函数定义为:

正弦(sin):对边/斜边

余弦(cos):邻边/斜边
正切(tan):对边/邻边
在这里,“对边”是指与给定角度相对的边,“邻边”是指与给定角度相邻的直角边,而“斜边”则是直角三角形的最长边。
假设我们有一个直角三角形,三条边的长度分别为a(一条直角边)、b(另一条直角边)和c(斜边)。为了找到与直角边a相邻的角(记为θ),我们可以使用以下公式:
sinθ = a/c
cosθ = b/c
tanθ = a/b
通过这些公式,我们可以计算出角度θ的值。但是,需要注意的是,这些公式给出的是角度的正弦、余弦或正切值,而我们需要的是角度本身。因此,我们需要使用反三角函数来找到角度。
2. 使用反三角函数计算角度
反三角函数是三角函数的逆运算。例如,arcsin(反正弦)是sin(正弦)的逆运算,arccos(反余弦)是cos(余弦)的逆运算,arctan(反正切)是tan(正切)的逆运算。这些函数允许我们从三角函数值找到对应的角度。
在计算器上,你可以使用arcsin、arccos和arctan函数来计算角度。但是,需要注意的是,这些函数返回的角度通常是以弧度为单位的,而不是以度为单位的。如果你需要得到以度为单位的角度,你可能需要将弧度转换为度(1弧度约等于57.296度)。
现在,让我们来计算直角三角形中的三个角度。
计算与直角边a相邻的角θ
1. 使用正弦函数:sinθ = a/c。通过计算器求出arcsin(a/c),得到θ的弧度值,然后将其转换为度。
2. 使用余弦函数:cosθ = b/c。通过计算器求出arccos(b/c),同样可以得到θ的弧度值,然后转换为度。由于sinθ和cosθ计算的是同一个角,所以这两种方法得到的结果应该是相同的(或非常接近,取决于计算精度)。
3. 使用正切函数:tanθ = a/b。通过计算器求出arctan(a/b),得到θ的弧度值,然后转换为度。这种方法通常用于计算非直角的角度,因为它不涉及斜边c。但是,由于我们已知所有边的长度,所以也可以使用这种方法来验证前面计算的结果。
计算与直角边b相邻的角φ
由于直角三角形的三个角度之和为180度(或π弧度),并且其中一个角度是直角(90度或π/2弧度),所以我们可以很容易地找到与直角边b相邻的角φ:
φ = 180度 - θ - 90度 = 90度 - θ
或者,如果你使用的是弧度制:
φ = π - θ - π/2 = π/2 - θ
计算直角
当然,直角本身就是90度(或π/2弧度),不需要任何计算。
3. 示例计算
为了更具体地说明这个过程,让我们来看一个示例。假设我们有一个直角三角形,其边长分别为a = 3、b = 4和c = 5(这是一个著名的3-4-5三角形,其角度可以轻松通过勾股定理或其他方法验证)。
计算与直角边a相邻的角θ:
sinθ = 3/5 ≈ 0.6
θ ≈ arcsin(0.6) ≈ 36.87度(或使用计算器上的相应函数得到的结果)
计算与直角边b相邻的角φ:
φ = 90度 - θ ≈ 90度 - 36.87度 ≈ 53.13度
直角自然是90度。
4. 注意事项
在使用计算器计算反三角函数时,确保你的计算器处于正确的模式(度数或弧度)。如果你得到的结果是以弧度为单位的,并且你需要以度为单位的结果,请记得进行转换。
在使用三角比时,确保你正确地识别了对边、邻边和斜边。这是正确计算角度的关键。
记住,对于任何直角三角形,其三个角度之和总是180度(或π弧度),其中一个角度总是直角(90度或π/2弧度)。这个性质可以用来验证你的计算结果是否正确。
总之,使用直角三角形的三条边来计算其三个角度是一个相对简单但非常有用的过程。通过理解和应用三角比以及反三角函数,你可以轻松地找到任何直角三角形的角度。这个过程不仅在几何学中有用,而且在许多其他领域(如物理学、工程学等)也有广泛的应用。
- 上一篇: 解密“日复一日,年复一年”背后的深层含义
- 下一篇: 揭秘:柬埔寨名称的由来与背后故事
-
 如何计算三角形的边长?资讯攻略11-02
如何计算三角形的边长?资讯攻略11-02 -
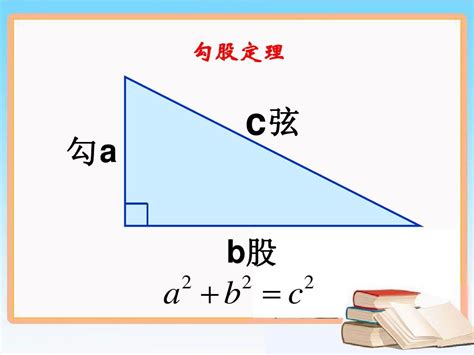 如何用直角三角形三边求解三个角度?资讯攻略01-04
如何用直角三角形三边求解三个角度?资讯攻略01-04 -
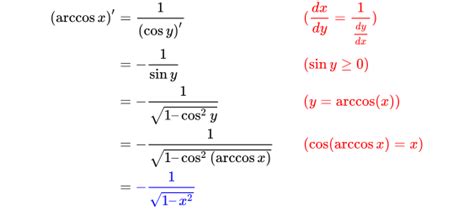 求y=arctan(x)的导数资讯攻略01-30
求y=arctan(x)的导数资讯攻略01-30 -
 轻松学会!小方巾的多种系法教程资讯攻略11-26
轻松学会!小方巾的多种系法教程资讯攻略11-26 -
 直线分割,双三角奇趣图解资讯攻略11-17
直线分割,双三角奇趣图解资讯攻略11-17 -
 家常三角粽制作秘籍:轻松学会的美味步骤资讯攻略11-27
家常三角粽制作秘籍:轻松学会的美味步骤资讯攻略11-27