直线分割,双三角奇趣图解
在浩瀚的几何世界中,每一条线、每一个形状都蕴含着无限的奥秘和可能性。今天,我们要探讨的是一个看似简单,实则充满趣味和思考的话题——如何用一条直线将一个平面切割成两个三角形。或许你会疑惑,一条直线如何能做到这一点?别担心,让我们一步步揭开这个几何谜题的面纱。
一、几何基础:直线的力量
在几何学中,直线是最基本、最纯粹的概念之一。它没有起点,没有终点,只是无限延伸的一条路径。直线的特性在于,它可以与其他几何元素相交、平行或重合,而这些关系往往能够产生意想不到的视觉效果和数学原理。
当我们提到“用一条直线切割平面”时,我们实际上是在探索直线与平面相交所产生的结果。想象一下,你手持一支笔,笔尖轻轻触碰纸面,然后滑动,留下了一道黑色的痕迹。这道痕迹就是直线在平面上的投影,而它正是我们进行切割的工具。
二、图形变换:从四边形到三角形
现在,让我们从一个简单的四边形开始。四边形是一个拥有四条边的多边形,它可以是正方形、长方形、菱形等。为了简化问题,我们可以先考虑一个正方形,因为正方形的四条边都相等,四个角都是直角,这使得它成为了一个理想的几何模型。
接下来,我们的任务是找到一条直线,使这个正方形被切割成两个三角形。看似简单的问题,却需要我们运用一些几何学的智慧。
首先,我们可以尝试从正方形的一个顶点出发,画出一条对角线。对角线是一条连接正方形对边中点的直线,它将正方形切割成了两个完全相等的三角形。这是最简单、最直接的方法。
但是,如果我们想要寻找更多可能性呢?是否还有其他直线能够满足这个条件?答案是肯定的。事实上,只要满足一定的条件,我们可以画出无数条这样的直线。
三、探索无限可能:直线与三角形的奥秘
让我们回到正方形的起点,但这次我们不局限于对角线。想象一下,如果我们从正方形的一个顶点出发,沿着任意方向画出一条直线,这条直线将会与正方形的另外两边相交。这三个交点将形成一个三角形,而剩下的部分(包括正方形的一个顶点和一条边)与直线也将构成另一个三角形。
这个发现让我们意识到,直线的方向和位置对于切割结果有着至关重要的影响。通过改变直线的角度和长度,我们可以创造出形状各异、大小不同的两个三角形。这种灵活性使得几何图形变换充满了趣味性和挑战性。
四、图形的艺术:创造与欣赏
当我们用一条直线将正方形切割成两个三角形时,我们不仅仅是在解决一个数学问题,更是在创造一种视觉艺术。这两个三角形可以是相似的,也可以是不同的;它们可以相互对称,也可以各自独立。每一种组合都构成了一幅独特的画面,展现了几何学的魅力和美感。
在这个过程中,我们还可以尝试用不同的颜色、线条或图案来装饰这两个三角形,使它们更加生动、有趣。这样的创作不仅锻炼了我们的想象力和创造力,还让我们更加深入地理解了直线与平面相交所产生的视觉效果和数学原理。
五、几何与生活的联系:无处不在的三角形
几何学不仅仅是数学家和物理学家的专利,它实际上与我们的生活息息相关。从建筑到艺术,从科学到技术,三角形无处不在地发挥着它的作用。
在建筑中,三角形被用作支撑结构,因为它具有稳定性和强度。无论是桥梁的拱形设计,还是建筑的屋顶结构,我们都可以看到三角形的身影。这些结构不仅美观大方,而且能够承受巨大的重量和压力。
在艺术领域,三角形同样扮演着重要的角色。画家们常常利用三角形的构图来引导观众的视线,营造出层次感和深度感。雕塑家们则通过塑造三角形的形态来展现作品的动感和力量感。
在科学和技术领域,三角形更是无处不在。从物理学中的力学原理到计算机科学中的图形处理算法,三角形都是不可或缺的基本元素。它们不仅帮助我们解决了许多实际问题,还推动了科学技术的进步和发展。
六、结语:几何之旅,未完待续
通过用一条直线将一个平面切割成两个三角形的探索之旅,我们不仅学到了许多几何学的知识和技能,还领略了数学的魅力和美感。在这个过程中,我们发现了直线与平面相交所产生的无限可能性,也感受到了数学与生活的紧密联系。
然而,这只是几何世界的一个小小角落。在更广阔的数学领域中,还有无数未知等待着我们去发现和探索。从平面几何到立体几何,从欧几里得几何到非欧几里得几何,每一个领域都充满了挑战和机遇。
让我们带着对几何学的热爱和好奇心,继续前行在这条充满未知和惊喜的数学之路上吧!愿每一个热爱数学的人都能在这条路上找到自己的归属和成就感!
-
 探秘海洋美味:全面图解海水虾的种类与奇趣资讯攻略11-06
探秘海洋美味:全面图解海水虾的种类与奇趣资讯攻略11-06 -
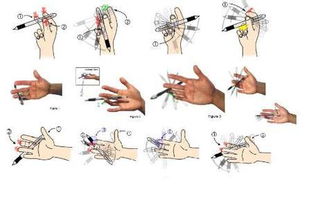 零基础转笔技巧大公开:超简易图解教程资讯攻略11-04
零基础转笔技巧大公开:超简易图解教程资讯攻略11-04 -
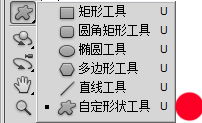 如何在Photoshop中绘制箭头资讯攻略11-27
如何在Photoshop中绘制箭头资讯攻略11-27 -
 超燃碰撞盛宴!探索奇趣撞车小游戏的无限玩法乐趣资讯攻略10-24
超燃碰撞盛宴!探索奇趣撞车小游戏的无限玩法乐趣资讯攻略10-24 -
 揭秘!蚂蚁庄园春分奇趣:为何‘蛋儿’成了主角?答案抢先看!资讯攻略10-25
揭秘!蚂蚁庄园春分奇趣:为何‘蛋儿’成了主角?答案抢先看!资讯攻略10-25 -
 惊悚奇趣:十万个冷尸兄简体中文版震撼来袭资讯攻略11-27
惊悚奇趣:十万个冷尸兄简体中文版震撼来袭资讯攻略11-27












