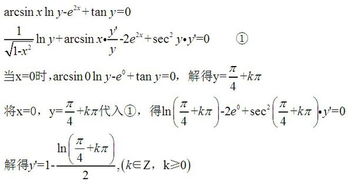求y=arctan(x)的导数
在数学的浩瀚宇宙中,隐藏着无数令人着迷的规律和秘密,而导数作为微积分中的璀璨明珠,更是揭示了函数变化率的奥秘。今天,我们就来揭开一个特别而迷人的数学面纱——“y = arctan(x)的导数”之谜。这不仅仅是一次数学公式的探索之旅,更是一场关于好奇心、逻辑推理与数学之美的邂逅。
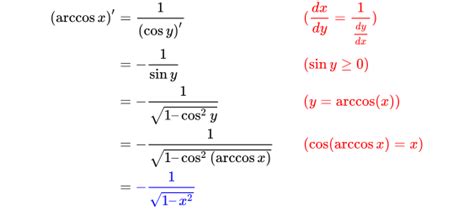
初识arctan(x):反三角函数的魅力
首先,让我们简要回顾一下arctan(x)的身份。arctan,全称反正切函数,是tan(x)的反函数。在直角三角形中,tan(x)表示对边与邻边的比值,而arctan(x)则是根据这个比值来找出对应的角度x。换句话说,如果tan(θ) = y,那么arctan(y) = θ。正因为它的存在,我们得以在数值与角度之间架起一座桥梁,探索几何与代数之间的和谐统一。
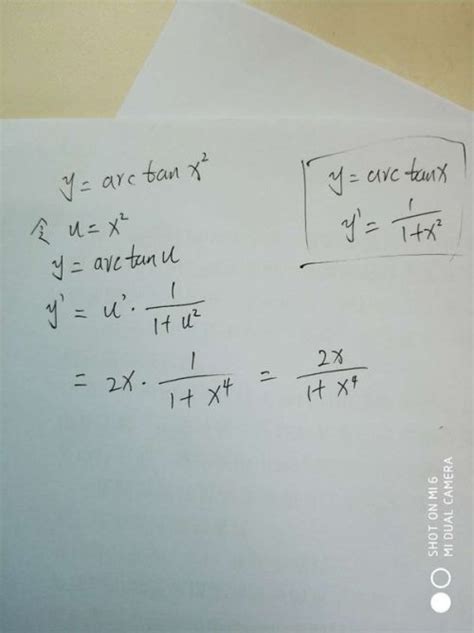
探秘导数:变化的艺术
导数,简而言之,就是描述函数在某一点上变化快慢的数学工具。想象一下,你正在驾驶一辆汽车,导数就像是速度计,告诉你当前时刻的瞬时速度。同样地,在函数的世界里,导数揭示了函数值随自变量变化的瞬间速率。那么,对于arctan(x)这样一个充满几何韵味的函数,它的导数会是怎样的风景呢?

推导之旅:逻辑与创意的碰撞
为了找到arctan(x)的导数,我们通常采用几何法或代数法。这里,我们将通过一种直观且富有创意的代数方法,一步步揭开它的神秘面纱。
首先,设y = arctan(x),这意味着tan(y) = x。根据正切函数的定义,我们有:
tan(y) = sin(y)/cos(y) = x
从上式可以解出sin(y) = x * cos(y)。接下来,我们对等式两边同时求导。但在此之前,需要注意到y是x的函数,因此在求导时需应用链式法则。
对sin(y)求导,得到cos(y) * dy/dx(因为y是x的函数,所以sin(y)对x的导数需要考虑y的变化)。对x * cos(y)求导,则得到cos(y) - x * sin(y) * dy/dx(这里同样应用了链式法则和乘法法则)。
将上述两部分相等,得到:
cos(y) * dy/dx = cos(y) - x * sin(y) * dy/dx
整理后,我们得到:
(1 + x²) * cos²(y) * dy/dx = cos(y) (因为sin²(y) + cos²(y) = 1,所以可以将x * sin(y)替换为√(1 - cos²(y)),但在本推导中直接利用原式更简洁)
进一步化简,得到:
dy/dx = cos(y) / (1 + x²)
但我们还需要将cos(y)表示为x的函数。回顾tan(y) = x,可以推出cos²(y) = 1 / (1 + tan²(y)) = 1 / (1 + x²)。因此,cos(y) = √(1 / (1 + x²))(取正值因为arctan(x)的值域在-π/2到π/2之间,此时cos(y)非负)。
代入上式,得到:
dy/dx = √(1 / (1 + x²))² / (1 + x²) = 1 / (1 + x²)
揭开面纱:y = arctan(x)的导数
经过一番精妙的推导,我们终于揭开了y = arctan(x)的导数的神秘面纱——它就是1 / (1 + x²)。这个公式简洁而优雅,不仅体现了数学内在的和谐之美,也彰显了导数作为变化率量度的强大功能。
深入思考:数学之美与实用
y = arctan(x)的导数不仅仅是一个数学公式,它背后蕴含的数学思想和方法论,对于理解自然界和工程技术中的许多问题至关重要。例如,在信号处理、控制系统、物理模拟等领域,arctan函数及其导数经常作为关键组件出现,帮助我们解决复杂问题,优化系统设计。
此外,这个推导过程本身也是一次逻辑思维和创造力的锻炼。它教会我们如何运用已知的数学工具和原理,通过逻辑推理和创造性思考,探索未知的数学世界。这种能力,无论是在学术研究还是日常生活中,都是极为宝贵的。
结语:数学之旅,未完待续
每一次数学探索,都是一次心灵的旅行。y = arctan(x)的导数之旅,让我们领略了数学的深邃与美妙,也激发了我们对未知世界的好奇心和探索欲。在这片充满无限可能的数学宇宙中,还有更多未知的奥秘等待着我们去发现、去解读。让我们带着这份热爱与敬畏,继续前行,在数学的世界里寻找更多的奇迹与答案。
通过这次对y = arctan(x)的导数的深入探讨,希望每一位读者都能感受到数学的魅力,不仅仅在于它的精确与严谨,更在于它激发人类智慧、推动科学进步的力量。数学,让生活更美好,让世界更精彩。
-
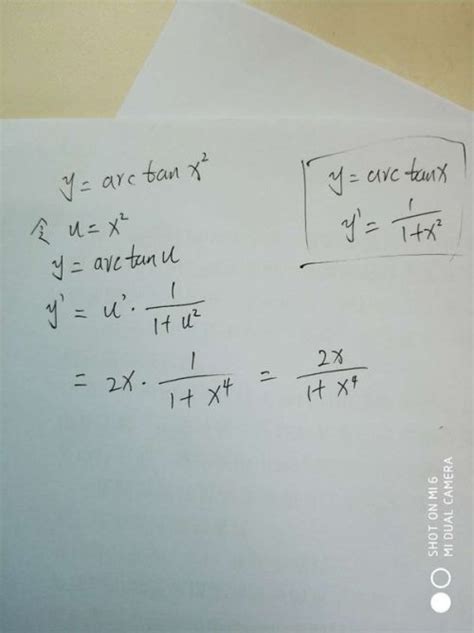 y关于arctan(x)的导数是什么?资讯攻略01-09
y关于arctan(x)的导数是什么?资讯攻略01-09 -
 探索tany的导数奥秘:揭秘其数学变化率资讯攻略03-15
探索tany的导数奥秘:揭秘其数学变化率资讯攻略03-15 -
 《宝可梦》中的X神、Y神、Z神分别指什么?资讯攻略01-22
《宝可梦》中的X神、Y神、Z神分别指什么?资讯攻略01-22 -
 揭秘二阶导数求解法:竟然如此轻松简单!资讯攻略02-08
揭秘二阶导数求解法:竟然如此轻松简单!资讯攻略02-08 -
 《语文必修二《离骚》第一段原文及注音详解》资讯攻略01-15
《语文必修二《离骚》第一段原文及注音详解》资讯攻略01-15 -
 生男孩的科学方法与技巧。资讯攻略11-07
生男孩的科学方法与技巧。资讯攻略11-07