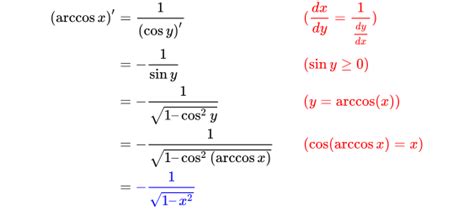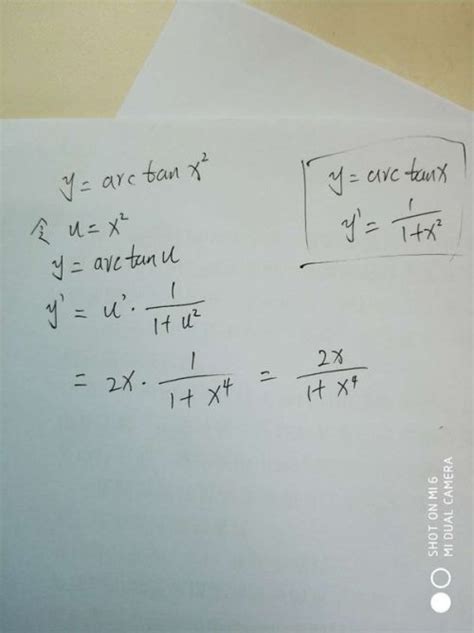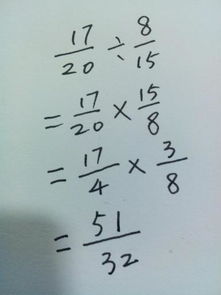探索tany的导数奥秘:揭秘其数学变化率
探究tany的导数:详细解析与推导
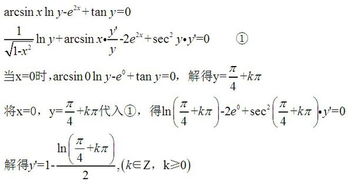
在微积分中,导数是描述函数值随自变量变化快慢的重要工具。对于基本初等函数,如三角函数,其导数具有特定的形式,并且在许多科学和工程应用中发挥着关键作用。本文将详细解析并推导tany(即正切函数)的导数,帮助读者深入理解这一概念。

首先,我们需要回顾一下正切函数的定义。正切函数tany定义为正弦函数siny除以余弦函数cosy,即tany = siny/cosy。为了求tany的导数,我们可以使用复合函数和商的导数规则。

一、使用商的导数规则求解

商的导数规则是微积分中的一个基本定理,它告诉我们如何求两个函数商的导数。对于函数u(x)/v(x),其导数(u/v)'可以通过以下公式求得:
(u/v)' = (u'v - uv') / v²
其中,u'和v'分别是u和v关于x的导数。
现在,我们将正切函数tany = siny/cosy看作是两个函数siny和cosy的商。根据商的导数规则,我们可以得到:
(tany)' = [(siny)'cosy - siny(cosy)'] / (cosy)²
接下来,我们需要求出siny和cosy的导数。根据三角函数的导数公式,我们知道:
(siny)' = cosy
(cosy)' = -siny
将这两个导数代入到商的导数规则中,我们得到:
(tany)' = (cosy·cosy - siny·(-siny)) / (cosy)²
= (cos²y + sin²y) / (cosy)²
然后,我们可以利用三角恒等式cos²y + sin²y = 1来简化这个表达式:
(tany)' = 1 / (cosy)²
另外,我们还可以利用正割函数secy的定义(secy = 1/cosy)来进一步简化这个导数表达式:
(tany)' = (secy)²
二、使用复合函数和链式法则求解
除了直接使用商的导数规则外,我们还可以通过复合函数和链式法则来求解正切函数的导数。这种方法虽然稍显复杂,但有助于我们更深入地理解微积分中的链式法则。
首先,我们将正切函数tany重新表示为arctan(tany)的复合函数。注意到arctan是反正切函数,它是正切函数的反函数。因此,我们可以将tany看作arctan(u)在u = tany时的取值。
现在,我们需要求出arctan(u)的导数。根据反函数的导数公式和链式法则,我们知道:
(arctan u)' = 1 / (1 + u²)
然后,我们将u = tany代入到这个导数表达式中,并注意到我们需要求出(tany)'来作为u'。但是,在这里我们采用一种稍微不同的方法:我们先求出d(tany)/dx,然后再将其代入到arctan(u)'的表达式中。
为了求出d(tany)/dx,我们可以使用链式法则:
d(tany)/dx = (d(tany)/dy) * (dy/dx)
由于我们在这里关心的是tany关于y的导数,所以dy/dx可以看作是1(即我们假设y就是x,或者更一般地说,我们在这里不考虑x和y之间的具体关系,而只关注tany关于其内部变量y的导数)。因此,上式简化为:
d(tany)/dy = (d(tany)/dy)
这个表达式看起来有些冗余,但它强调了我们在求导时关注的是函数内部变量的变化率。现在,我们可以利用前面已经求出的(tany)' = (secy)²来作为d(tany)/dy的值。
然后,我们将这个值代入到arctan(u)'的表达式中(注意这里u = tany,所以u' = d(tany)/dy):
(arctan(tany))' = 1 / (1 + (tany)²)
= 1 / (1 + (siny/cosy)²)
= 1 / (1 + (sin²y/cos²y))
= (cos²y) / (cos²y + sin²y)
= (cos²y) / 1
= cos²y
但是,这个表达式并不是我们想要的(tany)'的表达式。实际上,我们在这一步中犯了一个错误:我们试图将arctan(tany)的导数当作tany的导数来求,这是不正确的。arctan(tany)和tany是两个不同的函数,它们的导数也不相同。
为了纠正这个错误,我们应该回到原来的方法,即直接使用商的导数规则来求(tany)'。我们已经知道(tany)' = (secy)²,这是正确的表达式。
三、结论
综上所述,正切函数tany的导数是(secy)²,或者等价地说是1/(cosy)²。这个导数表达式在微积分、物理学和工程学等多个领域中都有广泛的应用。通过本文的详细解析和推导,读者应该能够深入理解正切函数导数的求解过程,并能够熟练掌握这一重要概念。
- 上一篇: TMO运营商的含义是什么
- 下一篇: 揭秘!“红尘多可笑,痴情最无聊”出自哪首经典歌曲?
-
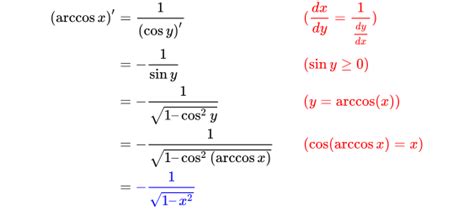 求y=arctan(x)的导数资讯攻略01-30
求y=arctan(x)的导数资讯攻略01-30 -
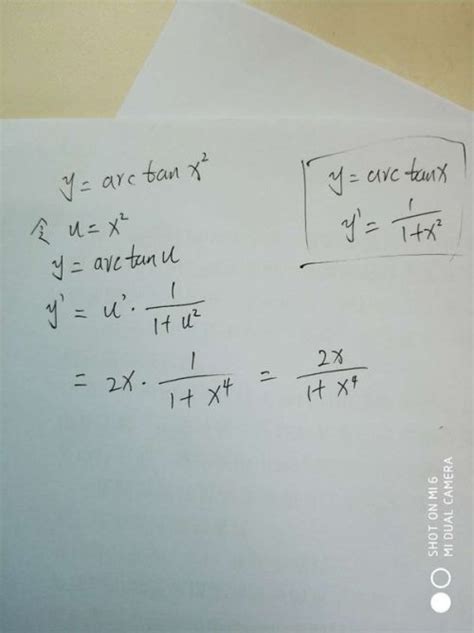 y关于arctan(x)的导数是什么?资讯攻略01-09
y关于arctan(x)的导数是什么?资讯攻略01-09 -
 揭秘二阶导数求解法:竟然如此轻松简单!资讯攻略02-08
揭秘二阶导数求解法:竟然如此轻松简单!资讯攻略02-08 -
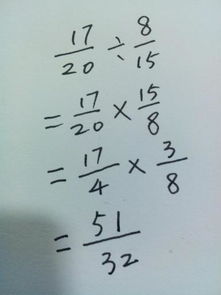 揭秘数学奥秘:20分之17如何巧妙除以15分之8?资讯攻略02-06
揭秘数学奥秘:20分之17如何巧妙除以15分之8?资讯攻略02-06 -
 揭秘:222背后的数字奥秘资讯攻略01-20
揭秘:222背后的数字奥秘资讯攻略01-20 -
 揭秘5544的质因数分解奥秘资讯攻略02-08
揭秘5544的质因数分解奥秘资讯攻略02-08