如何计算三角形的边长?
在探讨三角形的边长计算时,我们首先需要了解三角形的一些基本属性和概念。三角形是几何学中最基本也是最重要的形状之一,它由三条边和三个角组成。不同的三角形(如等边三角形、等腰三角形和不等边三角形)在计算边长时有着不同的方法和公式。以下是对三角形边长计算方法的详细介绍。
一、三角形边长计算的基础知识
三角形按照边长和角度的关系可以分为以下几种:

1. 等边三角形:三条边长度相等,三个角度都是60度。
2. 等腰三角形:有两条边长度相等,两个底角相等。
3. 不等边三角形:三条边长度各不相等,三个角度也各不相同。
在计算三角形的边长时,通常使用的工具有毕达哥拉斯定理(适用于直角三角形)、余弦定理和正弦定理(适用于任意三角形)。
二、直角三角形边长计算
直角三角形是最常见的三角形之一,它的一个角度为90度。在直角三角形中,如果已知任意两边的长度,可以通过毕达哥拉斯定理计算第三边的长度。
毕达哥拉斯定理
设直角三角形的两条直角边分别为a和b,斜边为c,则毕达哥拉斯定理的公式为:
c² = a² + b²
例如,如果已知直角边a=3,b=4,则斜边c的长度可以通过公式计算为:
c² = 3² + 4² = 9 + 16 = 25
c = √25 = 5
如果已知斜边c和一条直角边a,可以通过变形公式计算另一条直角边b:
b² = c² - a²
三、任意三角形边长计算
对于非直角三角形,通常使用余弦定理和正弦定理来计算边长。
余弦定理
余弦定理适用于已知三角形两边及夹角的情况。设三角形ABC的三边分别为a、b、c,角A、B、C为三角形的三个内角,则有:
c² = a² + b² - 2ab cos C
b² = a² + c² - 2ac cos B
a² = b² + c² - 2bc cos A
例如,如果已知三角形ABC的两边a=5,b=7,夹角C=60度,则第三边c的长度可以通过公式计算为:
c² = 5² + 7² - 2 × 5 × 7 × cos 60°
c² = 25 + 49 - 70 × 0.5
c² = 74 - 35
c² = 39
c = √39
正弦定理
正弦定理适用于已知三角形的两角及一边,或任意两角及所夹一边的对边的情况。设三角形ABC的三边分别为a、b、c,对应的角分别为A、B、C,则有:
a/sin A = b/sin B = c/sin C
这个公式可以用于计算未知边长。例如,如果已知三角形ABC的角A=30度,角B=45度,边c=10,则可以通过正弦定理计算边a:
a/sin 30° = 10/sin 45°
a = (10 × sin 30°)/sin 45°
a = (10 × 0.5)/√2/2
a = 5/√2/2
a = 5√2/2
四、特殊三角形的边长计算
等边三角形
对于等边三角形,所有边长相等,如果已知一边的长度,则其他两边的长度与之相同。
等腰三角形
对于等腰三角形,已知一条腰长和底边长,则另一条腰长与已知腰长相等。如果已知两腰长和夹角,可以通过余弦定理计算底边长。
五、边长计算的实践应用
三角形边长计算在多种实际问题中都有应用,例如建筑、测量、工程设计等。在测量领域,常常需要通过已知边长和角度来确定未知位置或距离。在建筑设计中,精确计算三角形的边长可以确保结构的稳定性和安全性。
六、边长计算的注意事项
1. 单位一致性:在计算过程中,确保所有边长和角度的单位一致,如米和弧度,或厘米和角度。
2. 角度取值范围:在计算时,角度通常使用弧度或度数表示,要注意取值范围。例如,在正弦和余弦函数中,角度取值在0到180度(或0到π弧度)之间。
3. 精度控制:在使用计算器进行计算时,要注意控制
-
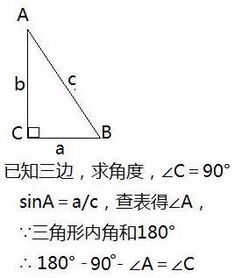 直角三角形边长求三角度,轻松学会!资讯攻略01-13
直角三角形边长求三角度,轻松学会!资讯攻略01-13 -
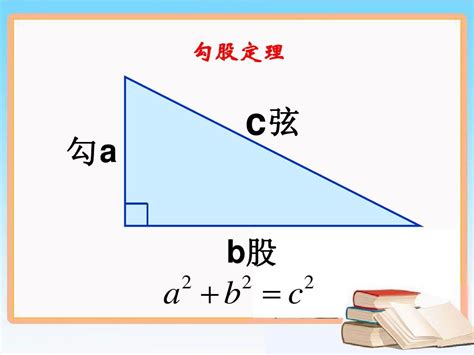 如何用直角三角形三边求解三个角度?资讯攻略01-04
如何用直角三角形三边求解三个角度?资讯攻略01-04 -
 轻松掌握:科学计算器使用指南资讯攻略10-27
轻松掌握:科学计算器使用指南资讯攻略10-27 -
 直线分割,双三角奇趣图解资讯攻略11-17
直线分割,双三角奇趣图解资讯攻略11-17 -
 打造完美三角肌:高效锻炼秘籍!资讯攻略11-03
打造完美三角肌:高效锻炼秘籍!资讯攻略11-03 -
 三角粽子应该如何包?资讯攻略10-29
三角粽子应该如何包?资讯攻略10-29











