MATLAB中轻松掌握假设检验技巧
MATLAB中假设检验的介绍

假设检验是统计学中的一种重要方法,通过样本数据对总体的某些特性进行推断,并判断提出的假设是否成立。在MATLAB中,假设检验功能强大且使用便捷,广泛应用于数据分析和科学研究中。本文将详细介绍MATLAB中的假设检验方法,包括单样本t检验、配对样本t检验、两样本t检验、Z检验、卡方检验等,并给出具体示例,帮助读者更好地理解和运用这些方法。
一、假设检验的基本概念
假设检验是概率意义上的反证法。通常我们根据问题的实际情况,提出两个相互对立的假设:一个是原假设(H0),表示我们试图拒绝的假设;另一个是备择假设(H1),表示我们试图证明成立的假设。通过样本数据,我们可以计算出检验统计量,并与临界值或p值进行比较,从而判断是接受原假设还是拒绝原假设。
在假设检验中,可能犯两类错误:
1. 第一类错误(弃真错误):原假设为真,但样本数据导致我们拒绝了原假设。
2. 第二类错误(取伪错误):备择假设为真,但样本数据导致我们接受了原假设。
显著性水平α通常用来控制第一类错误的概率,即当α=0.05时,表示我们有5%的概率犯第一类错误。
二、MATLAB中的假设检验方法
1. 单样本t检验
单样本t检验用于检验一个样本的均值是否等于一个已知值。在MATLAB中,可以使用`ttest`函数进行单样本t检验。
示例:
```matlab
% 样本数据
x = [41, 46, 47, 48, 50, 50, 50, 50, 50, 50, 48, 50, 50, 50, 50, 52, 52, 53, 55, 50, 50, 50, 52, 52, 53, 53, 53, 53, 57, 52, 52, 53, 53, 53, 53, 54, 54, 55, 68];
% 在1%显著性水平下,检验样本均值是否等于0
alpha = 0.01;
[h, p, ci] = ttest(x, 0, 'Alpha', alpha);
% 输出结果
fprintf('h = %d\n', h);
fprintf('p = %f\n', p);
fprintf('CI for mean(x) = [%2.3f, %2.3f]\n', ci(1), ci(2));
```
在上述代码中,`ttest`函数返回三个输出参数:`h`表示是否拒绝原假设(h=1表示拒绝,h=0表示不拒绝),`p`表示p值,`ci`表示均值的置信区间。
2. 配对样本t检验
配对样本t检验用于检验两个配对样本的均值是否存在显著差异。在MATLAB中,可以使用`ttest`函数进行配对样本t检验。
示例:
```matlab
% 配对样本数据
x = [775, 816, 834, 836, 858, 863, 873, 877, 885, 901]; % 新品种小麦产量
y = repmat(800, 1, 10); % 传统小麦品种平均产量(重复10次)
% 在5%显著性水平下,检验新品种小麦产量是否高于传统品种
alpha = 0.05;
[h, p, ci] = ttest(x, y, 'Alpha', alpha);
% 输出结果
fprintf('h = %d\n', h);
fprintf('p = %f\n', p);
fprintf('CI for mean(x-y) = [%2.3f, %2.3f]\n', ci(1), ci(2));
```
在上述代码中,`ttest`函数对两个样本`x`和`y`进行配对样本t检验,返回与单样本t检验相同的输出参数。
3. 两样本t检验
两样本t检验用于检验两个独立样本的均值是否存在显著差异。在MATLAB中,可以使用`ttest2`函数进行两样本t检验(当总体方差未知且相等时)。
示例:
```matlab
% 两个独立样本数据
- 上一篇: 轻松掌握:组织机构代码证查询全攻略
- 下一篇: 如何在一分钟内快速剥好石榴?
-
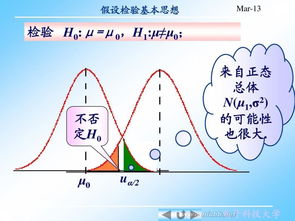 揭秘假设检验:一步步带你领略科学验证的奥秘资讯攻略11-03
揭秘假设检验:一步步带你领略科学验证的奥秘资讯攻略11-03 -
 问答式:如何轻松掌握用MATLAB软件绘制等高线图?资讯攻略11-14
问答式:如何轻松掌握用MATLAB软件绘制等高线图?资讯攻略11-14 -
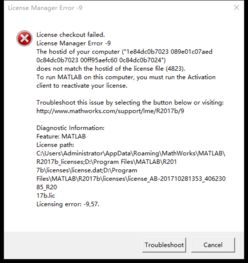 轻松解决MATLAB License Manager 错误 -114 的方法资讯攻略11-28
轻松解决MATLAB License Manager 错误 -114 的方法资讯攻略11-28 -
 揭秘!轻松检验Windows XP系统是否为正版的高效技巧资讯攻略04-13
揭秘!轻松检验Windows XP系统是否为正版的高效技巧资讯攻略04-13 -
 Excel求积公式:轻松掌握乘法运算技巧资讯攻略11-15
Excel求积公式:轻松掌握乘法运算技巧资讯攻略11-15 -
 PS技巧大揭秘:轻松打造炫酷闪图教程资讯攻略10-28
PS技巧大揭秘:轻松打造炫酷闪图教程资讯攻略10-28












