6的二进制表示是多少
6换算成二进制是110
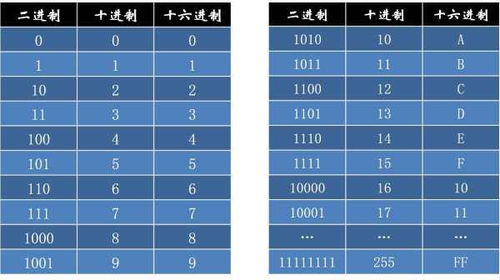
在计算机科学中,二进制是一种非常重要的数制,它是计算机内部数据存储和运算的基础。二进制只有0和1两个数字,这使得它在电子电路中实现起来非常简单和可靠。因此,了解如何将十进制数换算成二进制数是学习计算机科学的一个基本技能。在这里,我们将详细讲解如何将十进制数6换算成二进制数。

首先,我们需要明确二进制和十进制的基本概念。十进制是我们日常生活中最常用的数制,它使用0到9这十个数字来表示数值,每一位的权重是10的幂次方,从右到左依次为10^0、10^1、10^2……以此类推。而二进制则只使用0和1两个数字,每一位的权重是2的幂次方,从右到左依次为2^0、2^1、2^2……以此类推。

接下来,我们来看如何将十进制数6换算成二进制数。换算的方法有多种,这里我们介绍一种常用的方法——除2取余法。

第一步,将十进制数6除以2,得到商3和余数0。这个步骤可以理解为将6拆分成若干个2的幂次方之和,先找到最大的2的幂次方(这里是2^2=4)小于6,然后用6减去这个数,得到的结果再除以2,以此类推。由于6比4大但比8小,所以我们先取2^2,但此时并不直接减去4,而是通过除法来确定4的系数(即商为3,表示有1个4)。余数0表示在这一步中没有剩余的部分需要继续拆分。
第二步,将上一步得到的商3再除以2,得到商1和余数1。这一步是将3拆分成若干个2的幂次方之和,找到最大的2的幂次方(这里是2^1=2)小于3,然后用3减去这个数(实际上这一步是除法自动完成的,3除以2商1余1),得到的结果再除以2。余数1表示在这一步中剩余的部分是1个2^0。
第三步,将上一步得到的商1再除以2,得到商0和余数1。这一步是将1拆分成若干个2的幂次方之和,由于1本身就是2^0,所以直接得到余数1,商为0表示没有剩余的部分需要继续拆分。
至此,我们已经完成了所有的除法步骤,得到的余数序列是0、1、1。但是需要注意的是,这个序列是从下到上排列的,即最后得到的余数是最高位,最先得到的余数是最低位。因此,我们需要将这个序列翻转过来,得到正确的二进制数。
所以,十进制数6换算成二进制数是110。
为了验证这个结果的正确性,我们可以将二进制数110转换回十进制数进行检验。二进制数转换为十进制数的方法是:将每一位上的数字乘以对应的权重(即2的幂次方),然后将所有结果相加。对于二进制数110,最高位是1(对应权重2^2=4),中间位是1(对应权重2^1=2),最低位是0(对应权重2^0=1)。因此,110转换为十进制数的计算过程是:1×4+1×2+0×1=4+2+0=6。验证结果表明,我们的换算结果是正确的。
除了除2取余法之外,还有其他一些方法可以将十进制数换算成二进制数,比如乘2取整法、查表法等。但是无论采用哪种方法,其基本原理都是相同的,即利用二进制数的权重特点将十进制数拆分成若干个二进制数的和。
在实际应用中,二进制数的换算是一个非常重要的技能。特别是在计算机科学领域,了解二进制数的表示和运算对于理解计算机的工作原理、编写高效的程序以及进行数据加密等方面都具有重要意义。因此,我们应该熟练掌握二进制数的换算方法,并能够灵活运用它们来解决实际问题。
总之,十进制数6换算成二进制数是110。通过除2取余法我们可以轻松地将十进制数转换为二进制数,并可以通过将二进制数转换回十进制数来验证结果的正确性。掌握这个技能对于学习计算机科学和进行相关的应用研究都是非常重要的。
- 上一篇: 揭秘:亚父、尚父、仲父的真正含义是什么?
- 下一篇: 揭秘:'任用'一词背后的深层含义
-
 6转换为二进制是多少资讯攻略01-26
6转换为二进制是多少资讯攻略01-26 -
 二进制10101等于多少?资讯攻略01-11
二进制10101等于多少?资讯攻略01-11 -
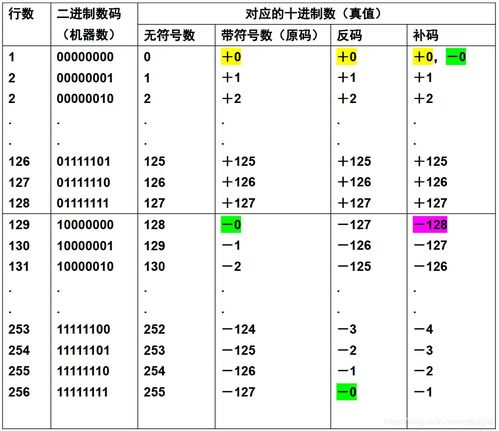 0的原码、反码、补码详解,一看就懂!资讯攻略02-01
0的原码、反码、补码详解,一看就懂!资讯攻略02-01 -
 郏县的邮政编码是多少?资讯攻略01-13
郏县的邮政编码是多少?资讯攻略01-13 -
 十六进制数转换为十进制数资讯攻略02-03
十六进制数转换为十进制数资讯攻略02-03 -
 揭秘:10101二进制背后的十进制真相资讯攻略01-28
揭秘:10101二进制背后的十进制真相资讯攻略01-28









