0的原码、反码、补码详解，一看就懂！

在计算机科学和数字电子中，原码、反码和补码是表示整数的三种不同方式，它们在计算机内部处理有符号整数时扮演着至关重要的角色。为了深入理解这些概念，特别是针对数字0的表示，让我们逐一探讨0的原码、反码和补码。

原码（Sign-Magnitude Representation）

原码是最直观的一种表示方法，它直接反映了数字的符号和大小。在原码表示法中，正数的原码是其绝对值对应的二进制形式，而负数的原码则是符号位（通常为最高位）设为1，其余位为该数绝对值的二进制形式。

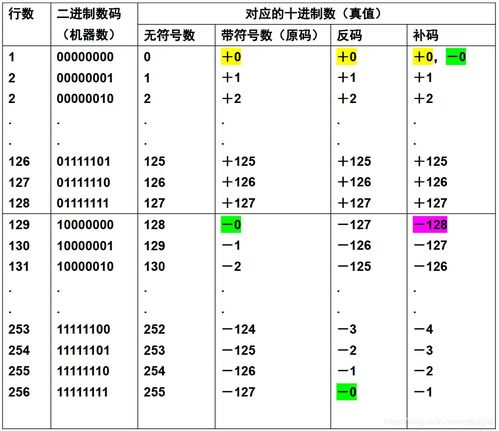
对于0而言，由于其既没有正也没有负，原码表示相对简单。在大多数情况下，0的原码是一个所有位都为0的二进制数。例如，对于一个8位二进制数，0的原码就是00000000。这种表示法直观且简单，但在进行算术运算时，尤其是涉及负数的加减运算时，会遇到一些问题，比如符号位参与运算导致的复杂性。

反码（One's Complement）

为了简化负数运算，人们引入了反码的概念。反码也称为一的补码，对于任意二进制数，其反码是将每一位都取反，即0变为1，1变为0。在反码表示法中，正数的反码与原码相同，而负数的反码则是其绝对值的二进制形式的每一位取反。

对于0来说，由于其原码就是所有位都为0的二进制数，因此0的反码也是所有位都为1的二进制数。以8位二进制数为例，0的反码就是11111111。然而，反码表示法虽然简化了负数的加法运算（通过加法实现减法），但在进行减法运算时仍需要额外的步骤来恢复正确的符号和数值，这导致了计算上的不便。

补码（Two's Complement）

补码表示法是目前计算机内部普遍采用的整数表示方法，它解决了原码和反码在运算上的不足。补码表示法的核心思想是利用二进制数的溢出特性来实现正负数的加减运算，从而避免了符号位的直接参与和额外的取反操作。

对于正数，其补码与原码相同。对于负数，其补码则是其反码加1。换句话说，负数的补码可以通过将其绝对值的二进制形式每一位取反后再加1得到。

对于0而言，由于其原码就是所有位都为0的二进制数，因此0的补码也是所有位都为0的二进制数，这与0的原码相同。这意味着在计算机内部，0的原码和补码在数值上是相等的，这一点与其他整数（特别是负数）的补码表示形成了鲜明对比。

补码表示法的优点在于它能够简化加减法运算，使得计算机硬件可以更加高效地执行这些操作。在补码表示法中，正数和负数的加减法运算都可以通过普通的二进制加法器来完成，而无需额外的电路来处理符号位或进行取反操作。此外，补码表示法还使得溢出检测变得更加简单，因为当运算结果超出表示范围时，溢出位会被自动丢弃。

0的补码表示法的实际应用

在计算机内部，0的补码表示法被广泛应用于各种算术运算和逻辑运算中。由于0的补码与原码相同，且都为所有位都为0的二进制数，这使得在计算机程序中处理0时变得非常方便。例如，在进行加法运算时，如果两个加数中有一个是0，那么结果仍然是另一个加数（无论是正数还是负数），这是因为0的补码与任何数的补码相加都不会改变那个数的值。

同样地，在进行减法运算时，如果减数是0，那么结果就是被减数本身。这也是因为0的补码与任何数的补码相减都等于那个数的补码本身（在补码表示法中，减法是通过加法实现的，即被减数的补码加上减数的补码的补码）。

此外，0的补码表示法还在计算机内部的逻辑运算中发挥着重要作用。例如，在进行与（AND）运算时，任何数与0的补码进行与运算的结果都是0的补码本身（即所有位都为0的二进制数）。同样地，在进行或（OR）运算时，任何数与0的补码进行或运算的结果都是那个数本身（因为0的补码的所有位都是0，而OR运算的规则是只要有一个输入位是1，那么输出位就是1）。

结论

综上所述，0的原码、反码和补码在计算机科学和数字电子中扮演着重要的角色。虽然0的原码和反码在表示上有所不同（原码是所有位都为0的二进制数，而反码是所有位都为1的二进制数），但0的补码与原码相同，这使得在处理0时变得更加方便和高效。补码表示法不仅简化了加减法运算，还使得溢出检测变得更加简单和可靠。因此，在计算机内部，补码表示法成为了处理有符号整数的首选方法。

通过深入理解0的原码、反码和补码的概念以及它们在计算机内部运算中的应用，我们可以更加深入地理解计算机如何处理整数运算，从而为我们编写更加高效和可靠的计算机程序提供有力的支持。