初等函数在其定义域内是否一定连续?
在数学的世界里,函数是一个非常重要的概念,它像是一座桥梁,连接着自变量与因变量之间的关系。当我们谈论初等函数时,通常是指那些最基础、最常见的函数类型,比如多项式函数、指数函数、对数函数、三角函数等。这些函数不仅在数学学习中频繁出现,在物理、工程、经济等多个领域也有着广泛的应用。在探讨这些函数时,一个经常被提及的问题就是:初等函数在其定义域内是否一定连续呢?

首先,我们需要明确什么是函数的连续性。简单来说,如果一个函数在某一点附近的函数值变化不大,即当自变量在该点附近发生微小变化时,函数值也只会发生微小的变化,那么我们就说这个函数在该点是连续的。而如果一个函数在其定义域内的每一点都连续,我们就说这个函数在其定义域内连续。

现在,让我们来逐一看看几种常见的初等函数是否满足这一性质。

多项式函数

多项式函数是我们最早接触的初等函数之一,它的形式通常是a_nx^n + a_(n-1)x^(n-1) + ... + a_1x + a_0这样的,其中a_n, a_(n-1), ..., a_1, a_0是常数,n是非负整数。多项式函数有一个非常优美的性质,那就是它在整个实数域R上都是连续的。无论你如何选择自变量x的值,多项式函数的值都会平滑地变化,不会出现跳跃或中断的情况。
指数函数
指数函数,特别是以自然常数e为底的指数函数e^x,也是初等函数中的一个重要成员。指数函数在其定义域(通常是实数域R)内同样是连续的。这意味着,无论x取何值,e^x的值都会连续地变化。当你增加或减少x的值时,e^x的值也会相应地平滑地增加或减少。
对数函数
对数函数是指数函数的逆函数,它通常以自然对数ln(x)或常用对数log(x)(以10为底)的形式出现。对数函数的定义域是正实数集(0, +∞),在这个定义域内,对数函数也是连续的。当你选择一个正实数作为自变量时,对数函数的值会连续地变化,不会出现间断点。
三角函数
三角函数,如正弦函数sin(x)、余弦函数cos(x)和正切函数tan(x)等,也是初等函数的重要组成部分。这些函数在它们的定义域内(通常是实数域R的某个子集)同样是连续的。例如,正弦函数和余弦函数在整个实数域R上都是连续的,而正切函数虽然在x=kπ+π/2(k为整数)处有间断点,但在其定义域内的其他部分仍然是连续的。不过,当我们谈论初等函数的连续性时,通常关注的是在其完整定义域内的连续性,因此我们可以说,在它们的完整定义域内(不考虑正切函数的间断点),三角函数是连续的。
至此,我们可能已经产生了一个初步的印象:初等函数在其定义域内似乎是连续的。然而,事情并没有那么简单。虽然上述列举的初等函数类型在其定义域内都是连续的,但这并不意味着所有的初等函数都是如此。
在数学上,“初等函数”这个词并没有一个严格的定义,它通常指的是那些通过有限次的基本运算(如加、减、乘、除、指数、对数、三角函数等)和有限次的复合运算得到的函数。但是,即使是这样得到的函数,也有可能在其定义域内存在不连续点。
例如,我们可以构造一个这样的初等函数:f(x) = (x^2-1)/(x-1)。这个函数在x=1处是不连续的,因为当x=1时,函数的分母为0,导致函数值不存在(或者说函数值趋于无穷大)。尽管这个函数是通过有限次的基本运算得到的,但由于在x=1处存在间断点,所以我们不能说这个函数在其定义域内是连续的。
此外,即使一个初等函数在其定义域内的大部分地方都是连续的,也有可能在某些特定的点上出现不连续的情况。这通常是由于函数在这些点上存在极限不存在、无穷大或无穷小的情况导致的。
因此,我们可以得出结论:虽然很多常见的初等函数在其定义域内都是连续的,但这并不意味着所有的初等函数都如此。一个初等函数是否在其定义域内连续,取决于它的具体形式和构造方式。
那么,为什么我们要关心初等函数的连续性呢?这是因为函数的连续性在数学和实际应用中都有着非常重要的意义。在数学上,连续性是微积分学的基础之一,它决定了函数是否可导、可积等关键性质。在实际应用中,函数的连续性也决定了我们能否通过微小的变化来预测函数值的变化趋势,这对于物理模拟、工程设计、经济预测等领域都是至关重要的。
综上所述,初等函数在其定义域内是否连续取决于具体的函数形式和构造方式。虽然很多常见的初等函数在其定义域内都是连续的,但我们也应该意识到存在不连续初等函数的可能性。因此,在学习和应用初等函数时,我们需要仔细分析它们的性质和定义域,以确保我们能够正确地理解和使用它们。
- 上一篇: 微信无法更换头像的原因及解决方法
- 下一篇: 泰国特产大揭秘:让你爱不释手的独特风味与手工艺
-
 探索tany的导数奥秘:揭秘其数学变化率资讯攻略03-15
探索tany的导数奥秘:揭秘其数学变化率资讯攻略03-15 -
 WPS Excel轻松掌握:如何快速求取数据中的众数资讯攻略11-25
WPS Excel轻松掌握:如何快速求取数据中的众数资讯攻略11-25 -
 揭秘:初等、中等与高等教育的全面解析资讯攻略11-17
揭秘:初等、中等与高等教育的全面解析资讯攻略11-17 -
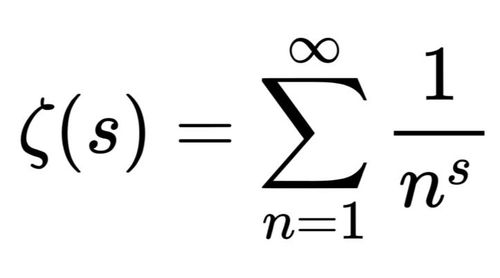 揭秘数学界圣杯:黎曼假设的深层意义与未解之谜资讯攻略10-24
揭秘数学界圣杯:黎曼假设的深层意义与未解之谜资讯攻略10-24 -
 Flash中attachMovie函数怎么使用?资讯攻略11-30
Flash中attachMovie函数怎么使用?资讯攻略11-30 -
 地下城与勇士游戏中如何使用函数钩子?资讯攻略12-02
地下城与勇士游戏中如何使用函数钩子?资讯攻略12-02