揭秘高中物理:动量定理的奇妙应用之旅

在高中物理的广阔天地里,动量定理无疑是一颗璀璨的明珠。它不仅是力学体系中的基本定理之一,更是解决诸多实际问题的重要工具。对于那些对物理充满好奇与探索欲的同学们来说,动量定理的应用无疑是一次智慧与趣味的双重探险。今天,就让我们一起走进动量定理的世界,揭开它神秘而又迷人的面纱。

一、动量定理的基本概述
动量定理表述为:物体动量的变化等于作用在物体上所有外力的冲量之和。用公式表示就是:Ft=mv₂-mv₁,其中F是作用力,t是作用时间,m是物体的质量,v₁和v₂分别是物体的初速度和末速度。这个定理揭示了力和时间对物体运动状态改变的共同影响,是牛顿第二定律在时间和空间上的积分形式。
二、动量定理在碰撞问题中的应用
碰撞是生活中常见的物理现象,从微观的粒子碰撞到宏观的汽车相撞,无不涉及动量定理的应用。在碰撞过程中,由于内力远大于外力,我们可以忽略外力的影响,认为系统动量守恒。利用这一特性,我们可以方便地求解碰撞前后物体的速度、动能等物理量。
例如,在光滑水平面上,有一质量为m₁的小球以速度v₀与另一静止的质量为m₂的小球发生完全弹性碰撞。根据动量定理和动量守恒定律,我们可以得出碰撞后两球的速度分别为v₁=[(m₁-m₂)/(m₁+m₂)]v₀和v₂=[(2m₁)/(m₁+m₂)]v₀。这一结论不仅帮助我们理解了碰撞过程中的动量转移,还为工程设计、安全防护等领域提供了理论依据。
三、动量定理在爆炸与反冲问题中的应用
爆炸与反冲是动量定理应用的又一重要领域。在这些过程中,由于内力远大于外力,系统动量同样可以认为守恒。通过巧妙地设计爆炸装置或反冲机构,我们可以实现能量的高效利用和目标的精确控制。
以火箭发射为例,火箭通过向后喷射燃料产生推力,从而实现向前飞行。这一过程中,火箭与燃料组成的系统动量守恒。根据动量定理,我们可以计算出火箭在不同阶段的速度和加速度,进而优化火箭的设计参数,提高发射效率。
四、动量定理在打击与拦截问题中的应用
在打击与拦截问题中,动量定理同样发挥着重要作用。无论是军事上的导弹拦截,还是体育比赛中的击球动作,都涉及到物体速度的快速改变和动量的传递。通过精确计算和分析,我们可以制定出有效的打击策略和拦截方案。
例如,在网球比赛中,运动员通过挥拍对网球施加力,使其获得足够的速度和旋转。根据动量定理,我们可以计算出运动员对网球施加的冲量大小和方向,进而优化击球动作,提高击球效果。
五、动量定理在交通事故分析中的应用
交通事故是现代社会中常见的安全隐患。利用动量定理对交通事故进行分析,可以帮助我们了解事故发生的机理和原因,为事故处理提供科学依据。
在交通事故中,车辆的碰撞往往伴随着动量的急剧变化。通过测量车辆碰撞前后的速度、质量等参数,我们可以利用动量定理计算出碰撞过程中的冲量大小和方向,进而分析出车辆的制动性能、驾驶员的反应时间等关键因素。这些信息对于提高交通安全意识、改进车辆设计具有重要意义。
六、动量定理在航空航天领域的应用
航空航天领域是动量定理应用的又一重要舞台。从火箭发射到卫星轨道调整,再到飞船返回地球,无不涉及动量定理的深刻应用。
在火箭发射阶段,通过精确计算火箭的推力、质量等参数,我们可以确定火箭的飞行轨迹和速度。在卫星轨道调整过程中,利用动量守恒原理,我们可以通过调整卫星的姿态和速度来改变其轨道。在飞船返回地球时,通过精确的制动和降落伞展开等操作,我们可以确保飞船安全着陆。这些技术的实现都离不开动量定理的支持和指导。
七、动量定理在日常生活中的应用实例
动量定理不仅在高科技领域大放异彩,在日常生活中也随处可见其身影。例如,当我们走路时,脚对地面的作用力会产生一个向后的冲量,同时地面也会对脚产生一个向前的反冲力,这个反冲力就是我们前进的动力来源。又如,当我们骑自行车时,通过蹬踏脚踏板对车轮施加力,使其获得足够的动量来克服阻力和重力向前运动。这些看似简单的日常现象背后,都蕴含着动量定理的深刻原理。
八、动量定理的学习方法与建议
对于广大高中生来说,学习动量定理不仅是为了应对高考的需要,更是为了培养自己的物理思维和解决问题的能力。在学习过程中,建议同学们注重以下几点:
1. 深入理解动量定理的基本概念和公式推导过程,掌握其物理意义和适用范围。
2. 通过大量练习和实例分析来
- 上一篇: 宝刀未老,英姿犹在:下一句如何续写传奇?
- 下一篇: 小孔成像原理能否用于观测日食?
-
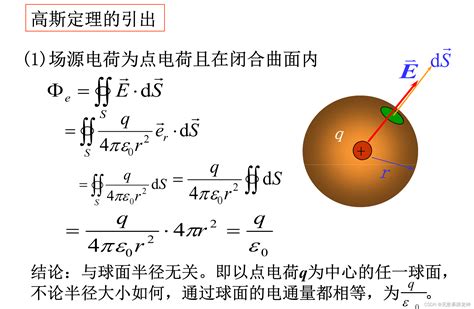 高等数学高斯公式到电磁学高斯定理的桥梁资讯攻略11-18
高等数学高斯公式到电磁学高斯定理的桥梁资讯攻略11-18 -
 揭秘拉斯定理:究竟是怎么一回事?资讯攻略11-30
揭秘拉斯定理:究竟是怎么一回事?资讯攻略11-30 -
 揭秘:数字111111111111背后的惊人秘密是什么?资讯攻略01-18
揭秘:数字111111111111背后的惊人秘密是什么?资讯攻略01-18 -
 高一物理揭秘:什么是质点、参考系与坐标系?资讯攻略10-29
高一物理揭秘:什么是质点、参考系与坐标系?资讯攻略10-29 -
 二项式定理核心知识点总结与推导详解资讯攻略11-13
二项式定理核心知识点总结与推导详解资讯攻略11-13 -
 如何准确描述物体的运动速度资讯攻略10-25
如何准确描述物体的运动速度资讯攻略10-25












