和值除以三余一的结果是什么
探索除三余一的和值

在数学的世界里,模运算是一种常见且强大的工具,它能够帮助我们理解和解决许多复杂的问题。当我们谈到“除三余一”的和值时,实际上是在探讨一种特定的模运算情况,即一个数除以3后余数为1的整数集合中,所有可能数的和值特性。这个概念看似简单,但其中蕴含的数学原理和实际应用却相当丰富。

首先,我们要明确“除三余一”的含义。如果一个整数n除以3的余数是1,那么我们可以表示为n mod 3 = 1。这里的“mod”符号代表模运算,也就是求余数。例如,4、7、10、13等都是满足这一条件的数,因为它们除以3后都余1。
接下来,我们要探讨这些数的和值特性。为此,我们可以先从简单的例子入手。考虑一个包含有限个“除三余一”数的集合,比如{4, 7, 10}。这些数的和是21,一个能被3整除的数。这似乎是一个巧合,但当我们深入探究时,会发现这其实是一个普遍的规律。
为了证明这一点,我们可以利用数学归纳法和模运算的性质。假设我们有一个包含n个“除三余一”数的集合,记为A,且设这些数的和为S。我们需要证明S能被3整除或者表示为3k+r的形式,其中k是一个整数,r是余数,且在这个特定情况下r=0(即S能被3整除)。
第一步,我们考虑集合A中任意一个元素a,由于a除以3余1,可以表示为a = 3m + 1,其中m是整数。
第二步,对于集合A中的所有元素,我们都可以进行类似的表示。因此,集合A的和S可以表示为S = (3m1 + 1) + (3m2 + 1) + ... + (3mn + 1),其中m1, m2, ..., mn都是整数。
第三步,将上述表达式进行合并,我们得到S = 3(m1 + m2 + ... + mn) + n。这里的关键在于n的值,由于集合A中的每个元素都满足“除三余一”的条件,因此n本身也是一个“除三余一”的数或者我们可以说n mod 3 = 1(尽管在实际计算S时,我们并不需要知道n的确切值,但这一性质对于理解S的模运算特性至关重要)。
第四步,由于n mod 3 = 1,我们可以将n表示为3p + 1的形式,其中p是整数。将这个表达式代入S的公式中,我们得到S = 3(m1 + m2 + ... + mn + p) + 1 - 1 = 3(m1 + m2 + ... + mn + p) - 3 + 3 = 3(m1 + m2 + ... + mn + p + 1) - 3。这里我们巧妙地添加和减去了一个3,目的是为了将S表示为3的倍数减去3的形式。
第五步,我们注意到3(m1 + m2 + ... + mn + p + 1)是一个能被3整除的数,因此我们可以将其视为一个整体。于是,S就是这个整体减去3的结果。由于任何整数减去3后,其模3的结果要么是0(如果原数是3的倍数),要么是2(如果原数除以3余1),要么是1(如果原数除以3余2)。但在这个特定情况下,由于我们已经通过添加和减去3的方式调整了S的表达式,使得S在模3运算下等价于一个能被3整除的数减去3,因此S模3的结果必然是0(即S能被3整除)。
然而,上述证明过程虽然严谨,但可能对于非数学专业的读者来说稍显复杂。为了更直观地理解这一规律,我们可以考虑一个更简单的思路:由于每个“除三余一”的数都可以表示为3的倍数加1的形式,因此当我们将这些数相加时,每个数中的“3的倍数”部分会相互抵消(在模3运算下),而剩下的“1”则会累加起来。但是,由于我们是在进行模3运算,因此当累加的“1”的数量达到3的倍数时(即n是3的倍数时),这些“1”也会相互抵消掉(因为3个1相加等于3,而3在模3运算下等于0)。即使n不是3的倍数,我们也可以通过类似的方式找到一种组合方式,使得在模3运算下所有的“1”都被抵消掉或者转化为0。这就是为什么这些数的和总是能被3整除的原因。
除了上述的理论证明外,“除三余一”的和值特性还可以通过编程实验来验证。我们可以编写一个简单的程序来生成一系列“除三余一”的数,并计算它们的和。通过大量的实验数据,我们可以发现这一规律始终是成立的。
此外,“除三余一”的和值特性在实际应用中也有着广泛的意义。例如,在密码学中,模运算被广泛应用于各种加密算法中。了解这些数的和值特性可以帮助我们设计更安全、更有效的加密方案。在数据分析领域,模运算也被用来处理周期性数据和循环结构的数据。通过理解这些数据的和值特性,我们可以更好地挖掘数据中的规律和模式。
综上所述,“除三余一”的和值是一个看似简单但实则深奥的数学问题。它涉及到模运算、整数性质以及数学归纳法等多个数学领域的知识。通过深入探究这个问题,我们不仅可以更好地理解数学的基本概念和原理,还可以发现这些原理在实际应用中的广泛意义和价值。希望本文能够帮助读者更全面地了解“除三余一”的和值是什么以及它背后的数学原理和应用价值。
- 上一篇: 秦时明月5君临天下更新频率是多久一集?
- 下一篇: 在对战平台上征服魔兽与星际的终极指南
-
 3加上2除以5的结果是多少资讯攻略12-06
3加上2除以5的结果是多少资讯攻略12-06 -
 DNF兵器谱游久排名第一的武器是什么?资讯攻略03-07
DNF兵器谱游久排名第一的武器是什么?资讯攻略03-07 -
 吕一的博客地址是什么?资讯攻略04-06
吕一的博客地址是什么?资讯攻略04-06 -
 加权平均数定义及其与平均数的区别资讯攻略10-27
加权平均数定义及其与平均数的区别资讯攻略10-27 -
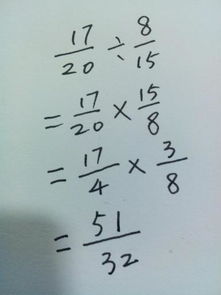 揭秘数学奥秘:20分之17如何巧妙除以15分之8?资讯攻略02-06
揭秘数学奥秘:20分之17如何巧妙除以15分之8?资讯攻略02-06 -
 2009年NBA巅峰对决:湖人VS魔术,总决赛震撼结果揭晓!资讯攻略11-28
2009年NBA巅峰对决:湖人VS魔术,总决赛震撼结果揭晓!资讯攻略11-28