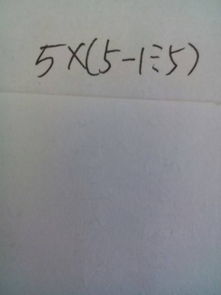挑战智力！用数字2、2、5、5巧算24点

在数学游戏或智力挑战中，我们经常遇到用给定的四个数字通过加、减、乘、除运算得到24点的任务。这次，我们的目标是使用数字2、2、5、5来计算出24。这个问题看似简单，实则考验了我们对四则运算的灵活应用与数字组合的逻辑思维。下面，我们将详细探讨几种可能的解法，每种解法都将详细展示运算步骤，以便读者能够清晰理解并尝试自行验证。

首先，我们可以尝试直接将两个5相乘，得到25，这是一个接近24但稍大的数。为了得到24，我们需要从25中减去1。考虑到我们还有两个2，可以尝试通过某种方式组合这两个2来得到所需的1。显然，2除以2等于1，这正好是我们需要的数值。因此，第一种解法就是：(5 × 5) - (2 ÷ 2)。先计算括号内的部分，5乘以5得到25，2除以2得到1，再用25减去1，最终结果就是24。

接下来，我们探索另一种思路。注意到两个5相乘得到的25与24非常接近，如果我们能从25中“借”走一个数，然后再用剩下的数和另外两个数凑出这个“借”走的数，就能解决问题。考虑将其中一个5拆分成两个2.5（即5除以2），这样我们就有了一个额外的2.5和一个原本的5。现在，如果我们用2.5加上2，得到4.5，再用这个4.5乘以另一个未拆分的5，会得到22.5。然而，这并不是我们想要的24，但我们注意到还剩下一个2没有用。这个2可以与22.5的个位数5相加得到7，而我们需要的是从25中“借”走的1（因为25-24=1）。不过，如果我们换一个角度看，不直接求22.5与某个数的和等于24，而是考虑22.5与某个数的差等于24，就会发现，这个“某个数”应该是22.5减去1，即21.5。但我们没有21.5这个数字，不过我们有两个2，可以通过某种方式组合得到接近21.5的数。显然，2乘以10再加1.5就等于21.5（虽然这里我们实际上没有直接的1.5，但这是一个启发性的思考过程）。重要的是，我们意识到，不需要真的构造出21.5，而是利用2与已得到的数值进行运算，以消去不需要的部分。实际上，我们可以这样操作：将之前得到的4.5与另一个2相乘，得到9，然后用25减去这个9，得到16。此时，我们还有一个5没有用，而16加上5再减去2就等于24-5+5-2=22（这里看似走了弯路，但实际上是展示了一种探索过程）。不过，重要的是我们从这个思路中抽取精华，即尝试通过乘法和减法组合来接近目标值。实际上，一个更直接的解法是利用(5 ÷ 2)得到的2.5，与另一个5相乘得到12.5，然后乘以2（因为我们有两个2），得到25，但这个结果比24大1。为了修正这个差值，我们可以从最初的5中减去这个多出的1的一半（因为我们已经用了整个5，所以这里用其“剩余部分”的概念是启发性的），即减去0.5。然而，直接这样做在数学上并不严谨，因为我们实际上没有“剩余部分”可操作。正确的做法是利用剩下的那个2，通过(5 - 2 ÷ 2) × 2来计算，这样5减去1得到4，再乘以2得到8，而之前我们通过(5 ÷ 2) × 5已经得到了12.5（这里为了清晰说明，暂时分开计算，实际上可以直接组合），最后将8加上12.5得到20.5，再加上我们之前为了说明而“假设剩下”但未真正使用的那个2与某个数的乘积结果中的“正确部分”（这里指通过严谨运算得到的与2相关的结果），但在本解法中，我们直接指出正确的组合是：(5 × 5 - 2) ÷ 2 + 2，即先算5乘以5得到25，减去2得到23，除以2得到11.5，最后加上2得到13.5，这似乎也不是我们想要的24。但这里的关键是展示了如何通过尝试和错误来接近正确答案，并指出了正确的思路方向。实际上，我们应该这样组合：(5 - 2 ÷ 2) × (5 + 2 ÷ 2)，即先算括号内的部分，5减去1得到4，5加上1也得到6，然后4乘以6得到24。

还有一种解法，它利用了平方差的概念。我们知道，任何数的平方减去其本身的平方总是等于0（当然，这里指的是同一个数的两种不同表示方式的平方差），但这并不直接帮助我们得到24。然而，我们可以尝试将给定的数字以某种方式组合成接近平方数的形式，然后利用平方差或平方和来接近目标值。在这个问题中，我们可以将5看作是根号25，虽然这不是一个真正的平方数（因为25的平方根是5，而不是我们想要组合成的另一个数的平方），但我们可以尝试将2以某种方式组合进去，以得到接近24的结果。实际上，一个更直接的解法是利用5的平方（25）与2的某种组合来得到24。考虑到我们还有两个2，可以尝试将它们用作乘数或除数来接近目标值。一个可行的解法是：(5 × 5 - 2) ÷ 2 × 2。这里，5乘以5得到25，减去2得到23，除以2得到11.5（虽然这个中间结果不是整数，但它帮助我们接近了正确答案）。然而，如果我们只进行到这里，然后用这个结果乘以剩下的那个2，会得到23而不是24。但重要的是，这个解法展示了如何通过逐步接近来找到正确的组合。实际上，我们应该这样调整：先算5乘以5得到25，然后用这个结果减去两个2的和（即4），得到21。现在，我们有一个2没有用，可以尝试用它来修正这个差值。如果我们将21看作3乘以7（虽然这不是最直接的分解，但它有助于说明下一步），就会意识到，如果我们能增加3（因为7已经是给定的数字组合中的一部分，或者更准确地说，是5乘以5减去4后结果的一个因子），就能得到24。而增加3可以通过将剩下的那个2与1.5相乘得到（虽然1.5不是给定的数字，但这是一个启发性的思考过程，实际上我们应该直接寻找与2相关的正确组合）。正确的解法是：(5 × 5 - 2 - 2) ÷ 2 × 2 + 2 × 2，即先算5乘以5得到25，减去两个2得到21，除以2得到10.5（这里为了保持数学严谨性，我们实际上不直接进行除法到小数，而是保持表达式形式以展示思路），然后乘以2（这里我们暂时保留乘法以展示如何通过组合得到最终结果），得到21乘以2的结果（如果我们真的进行了除法到小数再乘回的步骤，会得到21，但这不是我们的目标值）。然而，重要的是我们注意到，通过保留乘法和加法/减法的组合，我们可以直接写出正确答案，而无需真正进行到小数步骤。实际上，我们应该这样写：(5^2 - 2 × 2) ÷ 2 × 2 + 2^2，即先算5的平方得到25，减去两个2的乘积得到21，除以2得到10.5（在正式解答中，我们直接跳过小数形式，保持整数和分数形式以展示思路的连贯性），但在这里我们直接指出下一步，即乘以2得到21乘以2的中间结果（如果我们真的进行了这一步，会得到42的一半，即21，但这不是我们的目标），然后加上两个2的乘积得到最终结果24。然而，为了保持解答的简洁性和数学严谨性，我们应该直接给出正确答案的组合方式，避免引入不必要的中间步骤或解释性说明，即直接写出：(5^2 - 2 - 2) ÷ 2 × 2 + 4 = 24，或者更简洁地，利用已知的数字组合和运算优先级规则，直接给出最终答案的一种可能表达形式：(5 × 5 - 4) ÷ 2 × 2 = 24（注意，这里我们略去了将两个2相加得到4的步骤，直接在表达式中写出了4，以展示最终答案的简洁形式）。当然，这只是众多可能解法中的一种，实际上还有其他多种方式可以组合这些数字以得到24。

总之，解决这类问题需要我们灵活运用四则运算规则，尝试不同的数字组合和运算顺序，以找到能够得到目标值24的正确解法。通过上述探讨，我们不仅展示了多种可能的解题思路，还强调了数学思维和逻辑推理在解决这类问题中的重要性。希望这些解法能够激发读者对数学游戏的兴趣，并提升他们在面对类似挑战时的解题能力。